排序算法

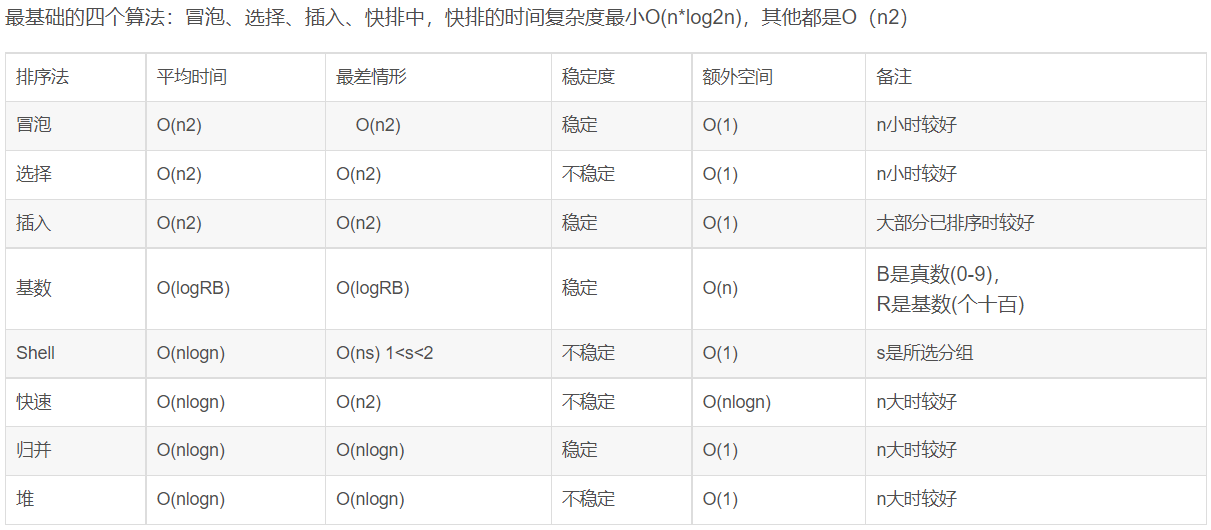
排序算法和复杂度

冒泡排序

是相邻元素之间的比较和交换，两重循环O(n2)；所以，如果两个相邻元素相等，是不会交换的。所以它是一种稳定的排序方法。不需要额外空间，空间复杂度O(1)。

伪代码

text

method bubbleSort(array A, integer N) // 标准版本, N表示循环次数，通常为数组长度
    for each R from N-1 down to 1 // 重复 N-1 次迭代
        for each index i in [0..R-1] // '未排序区域'，O(N)
            if A[i] > A[i+1] // 这两个不是非递减顺序
                swap(a[i], a[i+1]) // 在 O(1) 中交换它们

比较和交换需要的时间由一个常数限制，我们称之为 c。然后，在（标准）冒泡排序中有两个嵌套循环。外循环正好运行 N-1 次迭代。但是内循环的运行时间越来越短：
    当 R=N-1 时，(N−1) 次迭代（比较和交换），
    当 R=N-2 时，(N−2) 次迭代，
    ...，
    当 R=1 时，1 次迭代（然后完成）。

因此，总的迭代次数 = (N−1)+(N−2)+...+1 = N*(N−1)/2 (推导).
总时间 = c*N*(N−1)/2 = O(N^2).

点击执行，可以在控制台中查看可能的执行结果

选择排序

每一次循环都找出最小的元素，产生交换放在前面，两重循环O(n2)；举个栗子，5 8 5 2 9，第一遍之后，2会与5交换，那么原序列中两个5的顺序就被破坏了。所以不是稳定的排序算法。

不需要额外空间，空间复杂度O(1)。

text

method selectionSort(array A[], integer N)
  for each L in [0..N-2] // O(N)
    let X be the index of the minimum element in A[L..N-1] // O(N)
    swap(A[X], A[L]) // O(1)，X 可能等于 L (没有实际交换)
总计: O(N2) — 准确地说，它类似于冒泡排序分析。

点击执行，可以在控制台中查看可能的执行结果

插入排序

插入排序是在一个已经有序的小序列的基础上，一次插入一个元素。刚开始这个小序列只包含第一个元素，事件复杂度O(n2)。比较是从这个小序列的末尾开始的。想要插入的元素和小序列的最大者开始比起，如果比它大则直接插在其后面，否则一直往前找它该插入的位置。如果遇见了一个和插入元素相等的，则把插入元素放在这个相等元素的后面。所以相等元素间的顺序没有改变，是稳定的。

不需要额外空间，空间复杂度O(1)。

text

method insertionSort(array A[], integer N)
  for i in [1..N-1] // O(N)
    let X be A[i] // X is the next item to be inserted into A[0..i-1]
    for j from i-1 down to 0 // this loop can be fast or slow
      if A[j] > X
        A[j+1] = A[j] // make a place for X
      else
        break
    A[j+1] = X // insert X at index j+1

点击执行，可以在控制台中查看可能的执行结果

归并排序

归并排序是把序列递归地分成短序列，递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的段序列合并成一个有序的长序列，不断合并直到原序列全部排好序。

可以发现，在1个或2个元素时，1个元素不会交换，2个元素如果大小相等也没有人故意交换，这不会破坏稳定性。那么，在短的有序序列合并的过程中，稳定是是否受到破坏？没有，合并过程中我们可以保证如果两个当前元素相等时，我们把处在前面的序列的元素保存在结果序列的前面，这样就保证了稳定性。所以，归并排序也是稳定的排序算法。

text

method mergeSort(array A, integer low, integer high)
  // 要排序的数组是 A[low..high]
  if (low < high) // 基本情况：low >= high (0 或 1 个项目)
    int mid = (low+high) / 2	
    mergeSort(a, low  , mid ) // 分成两半
    mergeSort(a, mid+1, high) // 然后递归排序它们
    merge(a, low, mid, high) // 征服：合并子程

点击执行，可以在控制台中查看可能的执行结果

快速排序

快速排序有两个方向

左边的i下标一直往右走，当a[i] <= a[center_index]，其中center_index是中枢元素的数组下标，一般取为数组第0个元素
而右边的j下标一直往左走，当a[j] > a[center_index]。
如果i和j都走不动了，i <= j, 交换a[i]和a[j],重复上面的过程，直到i>j。
交换a[j]和a[center_index]，完成一趟快速排序。

在中枢元素和a[j]交换的时候，很有可能把前面的元素的稳定性打乱，比如序列为 5 3 3 4 3 8 9 10 11，现在中枢元素5和3(第5个元素，下标从1开始计)交换就会把元素3的稳定性打乱，所以快速排序是一个不稳定的排序算法，不稳定发生在中枢元素和a[j]交换的时刻。

text

int partition(array A, integer i, integer j)
  int p = a[i] // p 是枢轴
  int m = i // S1 和 S2 最初为空
  for (int k = i+1; k <= j; ++k) // 探索未知区域
    if ((A[k] < p) || ((A[k] == p) && (rand()%2 == 0)))  { // 情况 2+3
      ++m
      swap(A[k], A[m]) // 交换这两个索引
    // 注意我们在情况 1: A[k] > p 时不做任何事情
  swap(A[i], A[m]) // 最后一步，交换枢轴和 a[m]
  return m // 返回枢轴的索引
  
method quickSort(array A, integer low, integer high)
  if (low < high)
    int m = partition(a, low, high) // O(N)
    // A[low..high] ~> A[low..m–1], pivot, A[m+1..high]
    quickSort(A, low, m-1); // 递归排序左子数组
    // A[m] = pivot 在分区后已经排序
    quickSort(A, m+1, high); // 然后排序右子数组

排序算法 ​

冒泡排序 ​

选择排序 ​

插入排序 ​

归并排序 ​

快速排序 ​

堆排 ​

排序算法

冒泡排序

选择排序

插入排序

归并排序

快速排序

堆排